Introduction
For some reason, my sister’s stupid school gave her a homework to solve a peculiar sudoku puzzle for extra credits. it’s pretty annoying, and she just couldn’t figure it out, so I was now up for the task.
There is no way I’m gonna waste time solving a sudoku, but what I will do is sharpen those programming blades of mine… Anyways, enough about me, and more about the actual problem.
Sudoku Pie, Literally
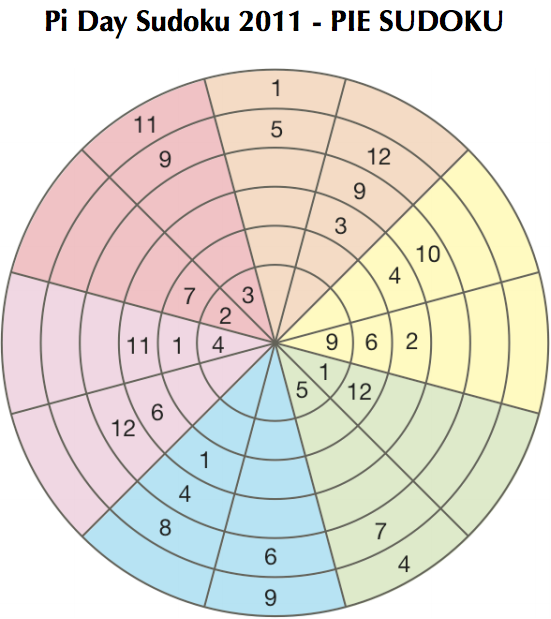
You get my point now.
The Ugly
First, I have already written a stupid sudoku solver that uses backtracking, but it didn’t work at all. So, instead of wasting time on that idea, I decided to first try my luck!
Going over all the empty slots, calculate the possible entries for each slot, then simply fill the slots randomly till the puzzle is solved!
"""
Created On: 3/12/15
"""
import random
import time
from copy import deepcopy
__author__ = 'mazyod'
def adjacent_container(i):
return i + (-1 if i%2 else 1)
def print_possibles(p):
for a in p:
for r in a:
print len(r), " ",
print ""
def check_puzzle_sane(new_s):
for i, a in enumerate(new_s):
adj = new_s[adjacent_container(i)]
if len(set(a+adj)) != 12:
return False
for i in xrange(len(new_s[0])):
k = []
for a in new_s:
k.append(a[i])
if len(set(k)) != 12:
return False
return True
s = [[5, 0, 0, 0, 7, 4],[1, 12, 0, 0, 0, 0], [9,6,2,0,0,0], [0,0,4,10,0,0], [0,0,3,9,12,0],[0,0,0,0,5,1], [3,0,0,0,9,11],[2,7,0,0,0,0],[4,1,11,0,0,0],[0,0,6,12,0,0],[0,0,1,4,8,0],[0,0,0,0,6,9]]
p = []
q = range(1,13)
def check(i, x):
for a in s:
if a[i] == x:
return True
return False
for a in s:
t = []
for i, v in enumerate(a):
n = filter(lambda x: x not in a and x not in s[adjacent_container(i)], q)
n = filter(lambda x: not check(i, x), n)
t.append(n)
p.append(t)
print_possibles(p)
new_s = s
i = 0
while not check_puzzle_sane(new_s):
new_s = deepcopy(s)
for o, a in enumerate(new_s):
for j in xrange(6):
if not a[j]:
ps = p[o][j]
a[j] = ps[random.randint(0, len(ps)-1)]
print new_s
print "holy cow"
Pretty stupid and shitty code, but I had limited time, and I just wanted to run anything. I ran that code on all 8 cores, and it still didn’t yield a result after a few hours of crunching.. Seemed like not a feasible solution :(
The Solution
I actually solved it on my second attempt, by just scratching my head a bit, and figuring out why this random generator was so bad.
It is really bad because once it picks a solution for a slot, it should update the other affected slots that this recently picked number is taken! That should cut down the iterations, I thought.
It was fairly simple to write this… First, by seeing the puzzle, all slots in the same color share a pool of possible numbers. It is the same for all slots. Then, the slots on the same ring share a pool themselves. For each slot, the possible numbers is the intersection of both.
n = [] # n is colors
for d, a in enumerate(s[::2]):
color = a + s[(d*2)+1]
n.append(set(filter(lambda x: x not in color, q)))
m = [] # m is rings
for w in xrange(6):
dart = []
for a in s:
dart.append(a[w])
m.append(q - set(dart))
n = filter(bool, n)
m = filter(bool, m)
print n
print m
With that in mind, just create these two pools, and for each slot, intersect the color pool with the ring pool that the slot is on, and now we have the reduced possible numbers!
Once you pick a number for the slot, remove it from both pools, and continue your loop. As simple as that.
The beauty here is that we don’t have to check the board each time, which further speeds up the process, since if we run out of possible values for a slot, that is a flag for us that we need to restart.
What really helped in this case, is that there is more than one solution! So, the random isn’t looking for a single answer among billions.
new_s = s
fail = True
while fail:
N = deepcopy(n)
M = deepcopy(m)
new_s = deepcopy(s)
fail = False
for c, a in enumerate(new_s):
color = int(c / 2)
for ring in xrange(6):
if not a[ring]:
poss = N[color] & M[ring]
if not poss:
fail = True
break
r = random.sample(poss, 1)[0]
a[ring] = r
N[color] -= {r}
M[ring] -= {r}
print new_s
print "holy cow"
Conclusion
That solver is really fast, runs in under 500 ms, and the problem is solved!